-
Best Australian Pokies Free No Download No Registration
Poker Tournaments Brisbane Casino
Tips No Deposit Pokies 2024
Deposit Casino Pokies Win Real Money Australia
Australia Casinos That Accept Skrill 2024
Commercial Hotel Werribee Pokies
Try Pokies in Australia Machines for Free
Bingo Bonuses AU
Australian Roulette Online Game
Poker AU Casino
Spotify Track Recommendation
*Team final project completed for Harvard’s Data Science 1 course, AC 209a, together with Phoebe Wong & Karina Huang*
Overview
Spotify is a major music streaming platform with over 191 million active users, 40 million songs, and 2 billion playlists (source). One key feature of Spotify is the song recommendations that populate your homepage, organized by theme and genre (Browse, Country, Hip Hop, etc.) Recommending songs to users is not just a core aspect of Spotify alone. In fact, every music streaming service has some kind of music recommendation algorithm, kickstarted by Pandora Radio back in the day, a service that would allow a user to customize their listening experience dynamically by upvoting or downvoting songs. Each music service provider is competing to give their listeners the joy of discovering new music, and there are a wide array of algorithmic approaches companies are taking.
This project specifically tackles the challenge of recommending a set of songs that best fits a playlist. A playlist is simply a sequence of songs that are selected by a user. They range in size from 0 to hundreds of songs that may adhere to common theme, or vary substantially. The inherent belief in recommending songs based on a playlist is that the playlists are a collection of songs that represent the musical taste of the listener, and a good recommendation algorithm should be able to capitalize on that. By suggesting appropriate songs to add to a playlist, users can explore new songs that are similar to songs they love without having to actively search for them.
In order to recommend songs that best fit a playlist, we have to look at songs that are ‘similar’ to existing songs in the playlist. We have the agency to measure similarity from a few different perspectives, such as co-occurrence, playlist features, and metadata of the song (e.g., genre, artists and other audio features).
To reiterate, the main purpose of this project was to create a song recommendation algorithm that takes in a playlist and returns a proportional number of suggested tracks. The structure of this webpage is intended to first bring the reader through the data that was used to generate a playlist recommendation algorithm. Then, we shall take a deeper dive into the specific models that were implemented to achieve this. Finally, we reflect on which approaches worked and which ones didn’t, and try to ruminate about why that might be the case.
Million Playlist Dataset
The main dataset in this project is the million playlist dataset, which includes a million user-generated playlists with ~66.3 million total tracks, ~2.2 million unique tracks and ~295 thousands unique artists on Spotify. The playlists were created during the period of January 2010 through October 2017. The dataset contains the names of the tracks, artists, and albums within each playlist, along with the duration of each track.
Spotify API
We were able to query the Spotify API to get metadata for a handful of songs. The way in which we interfaced with the API was through the package spotipy. The metadata we obtained spanned the following track features:
- acousticness
- artist popularity
- danceability
- energy
- instrumentalness
- key
- liveness
- loudness
- mode
- speechiness
- tempo
- time signature
- valence
Most of these features have unique definitions that can be found on Spotify’s website here.
Data Processing & EDA
Due to the immense volume of the dataset and our limited time, we scaled down the million playlists dataset to two subsets of data. The first was a dataset of approximately 27,000 playlists for which we were able to obtain complete track metadata. The second was a very small dataset of 100 playlists on which we implemented our models to make sure they were working as expected. The larger of the two was labeled “track_meta” while the smaller of the two will be referred to as “subset100.”
The track_meta dataset is very useful for visualizing some of the distributions of metadata. In particular, we picked out a handful of the aforementioned features to plot in the figure below:
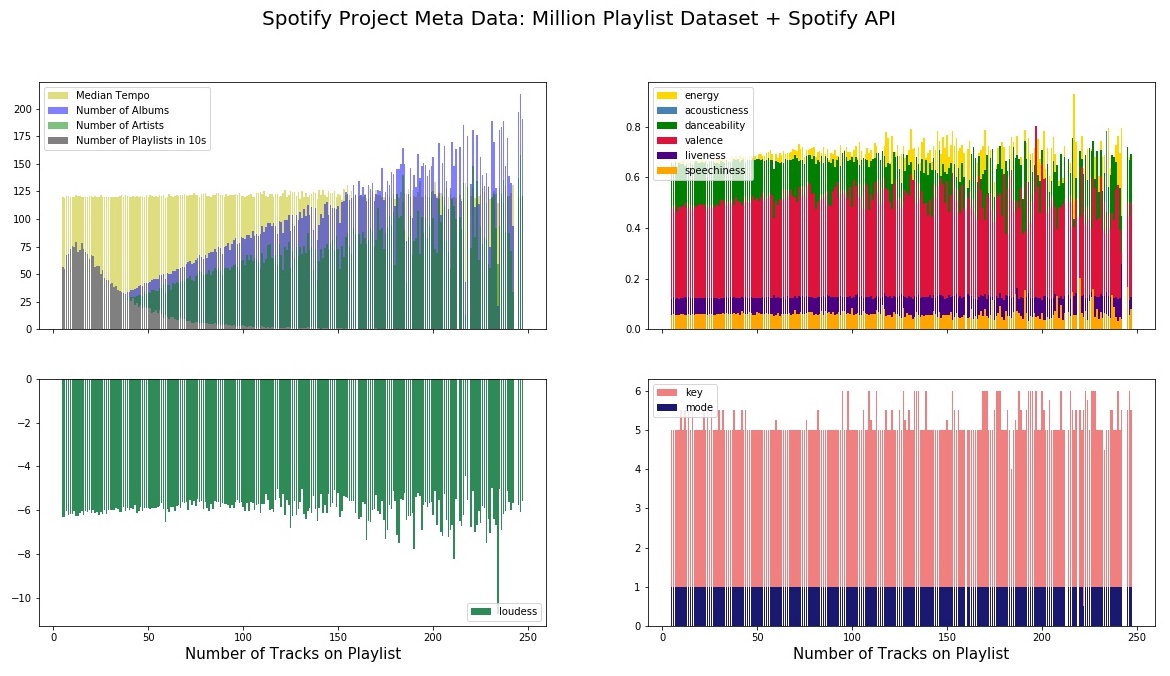
In the upper left plot one can see that the number of albums and artists increase linearly with the number of tracks as expected, and exhibit one-sided poisson like behavior when the expected value increases. The distribution of playlist lengths seems to peak around 20 songs or so, and the median tempo of songs in the playlist are all generally upbeat at around 120 bpm. Also interestingly, on the lower left plot, we can see that the median key and mode of a playlist are most often 5 and 1 respectively, which indicates that F-major is the most popular key signature for Spotify listeners in our sample. Coupled with large scores for energy and danceability from the upper right plot, it seems that listeners are into feel-good, happy music on average, which intuitively makes sense.
The subset100 dataset was a great way to take a closer look at the distributions of the size of playlists, number of albums, and number of artists:
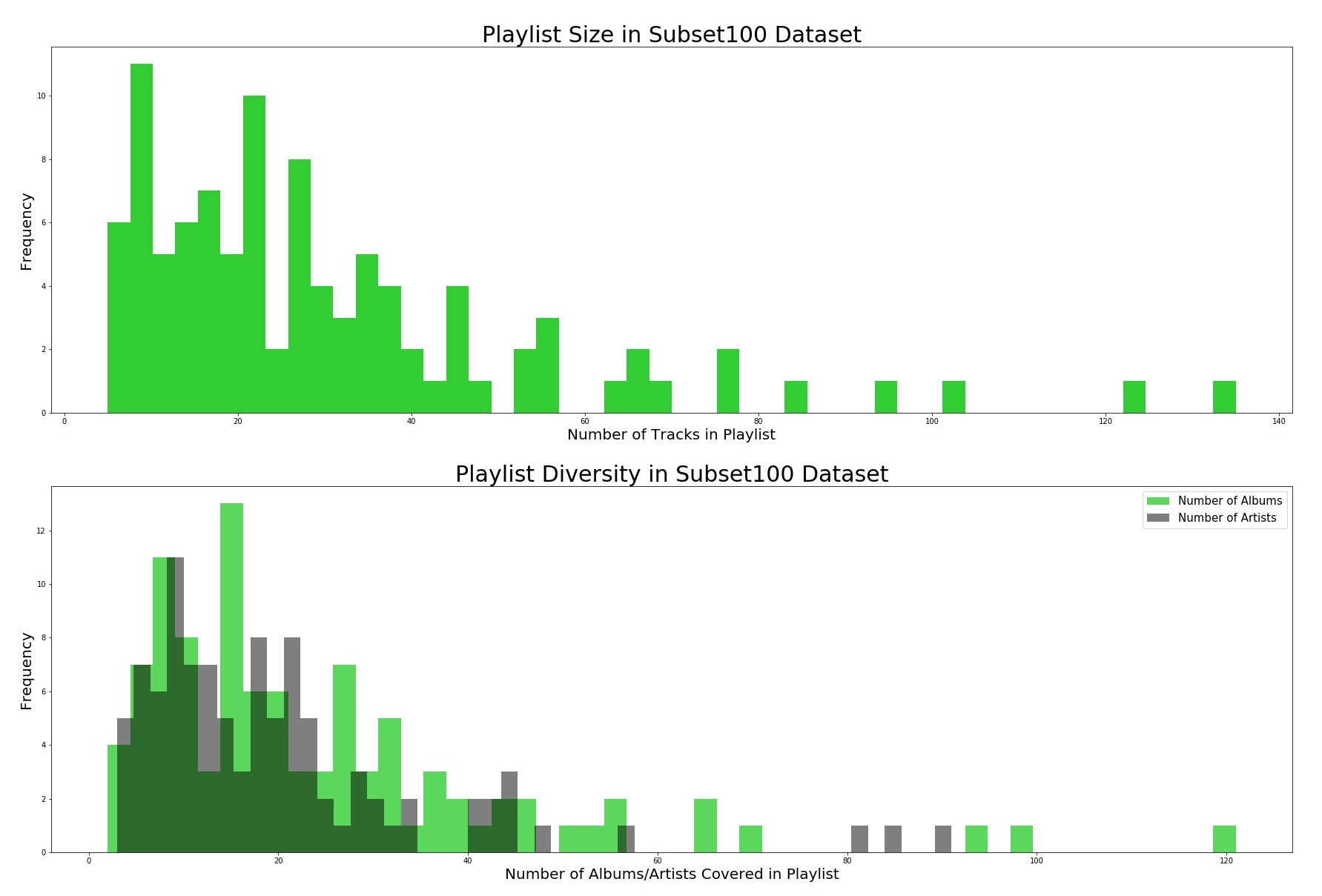
These figures validate that the average playlist size lies around 20 songs, with a little extra redundancy in the numbers of albums and artists as evidenced by the subtle shift in peak.
Metrics
Our data is in the form of multiple playlists of varying lengths. The way we partitioned the data was to split each playlist into training, validation, and test sets, where the each model’s ability to predict the “held out” songs in the validation set was used tune the hyperparameters of that model. We used the following metrics to evaluate our models, based on Spotify RecSys Challenge rules, in which participants had an identical task to our project goal.
R-Precision
R-precision is the number of retrieved relevant tracks, R, divided by the number of known relevant tracks (i.e., the number of withheld tracks), G. This metric rewards total number of retrieved relevant tracks (regardless of order), and is computed as follows:
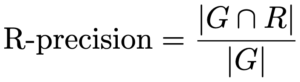
NDCG
Discounted cumulative gain (DCG) measures the ranking quality of the recommended tracks. Put simply, the metric increases when relevant tracks are placed higher in the list.
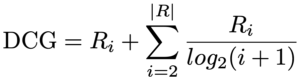
*Note that the variable R_i for each relevant track in the expression above can be thought of as an indicator variable.
Normalized DCG (NDCG) is determined by calculating the DCG and dividing it by the ideal DCG, in which the recommended tracks are perfectly ranked.
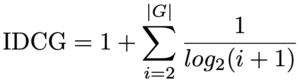
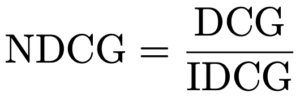
An NDCG of 1 means that the recommendation algorithm is working perfectly, and an NDCG of 0 occurs when the algorithm has not recommended any tracks that were in the holdout set.
Collaborative Filtering
Collaborative filtering generally refers to a set of algorithms that try to predict user preferences. The logic is simple, yet the execution is powerful. These algorithms are employed everywhere, from e-commerce websites, to video streaming services like YouTube, and of course, music streaming services like Spotify use them too. The first type of collaborative filtering that we implemented was an example of a memory-based, user-item algorithm. Memory-based means we are performing a one-off calculation, not optimizing. User-item means that we are taking user information to give item recommendations. Essentially, this algorithm uses a similarity metric to compare the current user’s preferences with all other user preferences, and then recommends non-redundant items that other users with similar preferences enjoy. The specifics of the implementation are outlined in the next section.
Implementation
Using the 100 playlist dataset, we first created a binary-sparse matrix encoding whether or not a given song was in a given playlist. The rows of the matrix were unique playlist id’s and the columns were unique song id’s. Given the sparsity and size of the matrix, we transformed the matrix into a Compressed Sparse Row (CSR) format to obtain an organized data representation with reduced size.
Next, to compare user preferences we used cosine similarity as a similarity index, which is essentially a dot product of each of the rows of the matrix. A dot product closer to 1 means the user preferences are very similar, and vice versa. To generate a set of recommendations, we used a k-NN algorithm with cosine similarity as the distance metric between vectors. For the hyperparameter k, we simply went with a high number because we don’t know a piori how many recommendations we give will be redundant.
Once the set of recommendations was generated, we only kept the first n recommendations, where n was a multiplicative factor, q, of the number of songs in the holdout set (in our case q = 15). This was to ensure we could make a fair comparison across playlists of different sizes, without this standardization, smaller playlists would have fewer songs in the holdout set to identify as relevant, thus inflating the R-Precision.
Model Performance
![]()
Our k-NN collaborative filtering model achieved a 7.7% R-Precision and an 8.0% NDCG. Averaging these two scores together, we get an overall score of 7.87%. We treated this as a baseline for our subsequent efforts.
Content-Based Filtering
Like collaborative filtering, content-based filtering generally refers to a set of algorithms that try to to predict user preferences. Content-based filtering, however, uses metadata from the products themselves to find similar products to those the user has expressed an interest in. This can be advantageous in situations where data on user preference is sparse, and allows for greater flexibility in determining how items are similar (through feature engineering).
Implementation
First, we built a matrix with unique tracks as rows, and features associated with those tracks as columns. Because the feature set was very heterogeneous (i.e. the scales of different features varied considerably), we normalized the rows and used cosine similarity to get measure of how similar tracks were to each other. To perform the prediction, we iterated through each playlist and selecting the top (q*n)/L recommendations for each song, where L is the length of the playlist. This generated a recommendation list of length q*n, where as a reminder, q is a multiplicative factor we set to be 15, and n is the number of tracks in the holdout set.
Model Performance

The content-based filtering model achieved a 4.88% overall score on the 100 playlist dataset, and a 3.78% score on a 1000 playlist dataset. Therefore, the content-based model performed worse than the baseline k-NN collaborative filtering model.
k-Means Clustering
k-Means clustering is an unsupervised machine learning algorithm used to group similar data. The algorithm is unsupervised because there are no labels associated with the datapoints indicating which cluster they belong to, or even how many clusters there should be. The grouping is done by specifying the number of clusters, k, and iteratively moving the cluster centroids through a process of assignment and averaging until the average distance of all datapoints to their respective centroid is globally minimized (i.e. when the algorithm converges). The advantage of using this algorithm is that the higher dimensionality space in which the clusters reside may yield more information about the relationship between groups of tracks than a dot product would. The implementation is outlined in detail in the following section.
Implementation
The first step in implementing the k-Means model was to run the clustering algorithm to group similar tracks. We pooled all of the tracks from the training portions of the playlists, including duplicates because the repeated tracks hint at the popularity of each song. In order to determine the number of clusters that best represent the different classes of tracks, we calculated a distortion curve (also called elbow curve), which measures the sum of within cluster squared distances. The figure below shows the distortion curve corresponding to the 100 playlist subset. In general, we did not observe a sharp elbow turn, so in order to avoid overfitting and save computational time, we chose k = 8.

Once we had the clusters, for each playlist we tabulated three values that formed the stages in which songs were chosen to be recommended. The order goes as follows:
- Most popular cluster label
- Most popular artist within cluster
- Most popular song by that artist within cluster
This is best internalized through an example. Suppose we have playlist A with 10 songs in it. Of these songs, seven belong to cluster 1, two belong to cluster 5, and one belongs to cluster 3. Cluster 1 is the most populous cluster, and therefore we would choose the most popular song from the most popular artist within cluster 1 to recommend first. Then we would pick the next popular song by that artist, etc. until we run out of songs by that artist within the cluster. At that point we move to the second most popular artist within the cluster, and repeat the process. Finally, if we exhaust all options from the cluster that are represented in the playlist (i.e. we have no second most common cluster), we determine the next most similar cluster through euclidean distance, and start recommending songs from that cluster.
At this point, we implemented the aforementioned clustering process to generate predictions, but our validation set scores were quite low (on the order of 2-3%). We postulated that perhaps clustering based on track metadata was too agnostic of artists, in that artists may have dissimilar songs in the feature space, yet their songs would appear multiple times in the same playlists anyway. As such, we decided to first recommend songs from artists that the user clearly liked, meaning the artist popped up 3 times or more in the training set. After these recommendations, we proceeded to fill the rest of the recommendation list with the clustering approach. This boosted the model performance significantly, as will be reported in the next section.
Model Performance
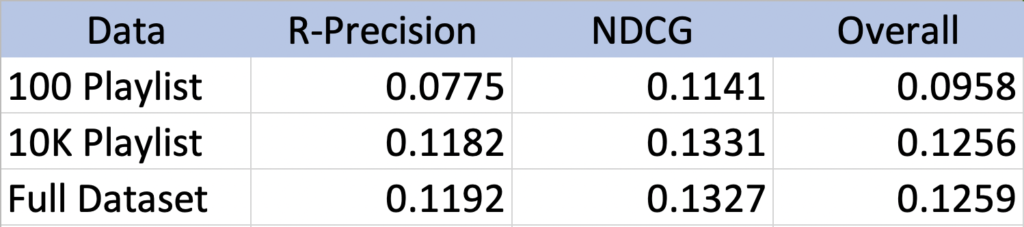
The model’s performance on the 100 playlist dataset was 9.58%, a marked improvement from the baseline model. When tested on the full dataset, however, this raised to 12.59%, indicating that the dataset we used for baseline comparison is small enough to where there is variance in the model performance. Either way, we believe this approach was more intricate and successful than co-occurrence collaborative filtering alone.
ALS Matrix Factorization
Alternating Least Squares (ALS) Matrix Factorization is another example of a recommendation system within the class of collaborative filtering algorithms. In our case, we used a version of the algorithm that works well with implicit data, which is any kind of information gathered from user behaviors, instead of an explicit user rating or score for each item. Alternating Least Squares refers to the loss function, as will be illuminated in the next section. In our case, the primary advantage of using this algorithm is that we can decompose a set of tracks into latent factors that characterize the songs. These latent factors allow for the comparisons of songs in a much more efficient manner than the k-NN co-occurrence approach from before. The disadvantage is that there is a loss in interpretability. We don’t truly know what the latent factors represent, but for our purposes, the most important outcome is that the user enjoys the songs we recommend, so accuracy is key.
Note that in the following sections, we will adhere to the general terminology of referring to “users” and “items.” When placed in the context of song recommendation, the users correspond to playlists, and the items are songs (think of it as how matching users to items is equivalent to matching playlists with songs). Also note, the graphics in this section were drawn from this fantastic source that was a vital aid in helping us understand how to use this algorithm.
Implementation
The main idea behind matrix factorization is to split up (factor) a user-item matrix of shape u x i into two rectangular submatrices of shapes u x f and f x i respectively, where f represents the number of latent factors. This is outlined in the colorful schematic below:

The number of latent factors is a hyperparameter we have the freedom to choose. Through cross-validation we chose f to be 15. After splitting up the user-item matrix, we ran the following steps:
- Initialize the submatrices with random, standard gaussian noise
- Define a loss function
- Iteratively adjust one submatrix at a time until they minimize the loss (a.k.a, until they multiply together to reproduce the original user-item matrix).
The loss function we used, pictured below, has a few key components:
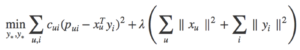
Going left to right, let us unpack the terms in the loss function. The first term, c_{ui}, is a measure of confidence in how much the user liked the item, and typically has the functional form given below:
![]()
Essentially, the confidence is set to have a baseline of 1, modulated by a feedback parameter, r, that is scaled according to α. In song recommendation systems, the feedback is usually in the form of play count – if someone plays a song in their playlist more frequently, the greater confidence that we have they actually like the song. Unfortunately, we did not have access to this information, and so we set the confidence to be a fixed value for each song that appears in the playlist, and 1 for songs that does not appear in the playlist.
The second term, p_{ui}, is a measure of user preference. Preference is simply a binary indicator variable that is switched on when a song is in a playlist, and off when it is not. This is summarized in the functional form displayed below:
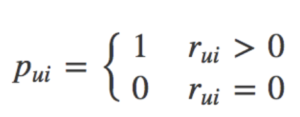
Next we have x_u and y_i, two rows of the submatrices, that when multiplied together are meant to match the preference term (the corresponding element in the original user-item matrix). The squared difference between this estimation and the true preference is weighted by the confidence to provide the main core of the loss function. The terms that follow are regularization terms, scaled by the regularization parameter, λ , so as to prevent the algorithm from overfitting to training data, ensuring its generalizability.
Once the algorithm converges, we are left with a set of submatrices linking users with items (playlists with songs). Therefore, for each playlist, we can take a dot product with each song that the playlist does not have, to generate an ordered list of songs that have very similar latent factors to the playlist. The last remaining step is to take the top n songs from that ordered list and we have our recommendations!
Model Performance
![]()
The ALS matrix factorization model performance completely outshined the previous approaches. The overall score was 19.5%, indicating that the latent factors were much more effective at characterizing playlist/song similarities than just track to track similarity or co-occurrence alone.
Discussion
Overall, the experience of coding a playlist recommender was extremely rewarding. The problem is unique for a few reasons. First and foremost, the dataset is very atypical. As the data came from multiple sources, we had a mix of datatypes coming from all sorts of distributions that were defined on very different domains. This made content-based filtering a lot harder, as we had to make sure we selected appropriate meta data and scaled the features carefully. A second reason this project was challenging was due to the non-traditional response variable. Fot data that comes with labels, it easy to split up into training and validation sets. For the spotify data, we not only had to make sure we stratified the samples on playlist id, we also had a non-traditional response variable in the form of a hold-out set. This led us to use metrics that catered specifically to this type of recommendation problem. The real growth and knowledge came from working to implement the following models, so without further ado we shall comment on our experiences with each of them.
Model Comparisons
Unfortunately, due to time and computer processing limitations, we were not able to do a fair comparison between models on a dataset larger than 100 playlists. However, we did test individual models on larger datasets, up to tens of thousands of playlists.
k-NN Collaborative Filtering vs. Content-Based Filtering
Our expectations for kNN collaborative filtering were low. We thought that we would need more nuanced information about a playlist, rather than some measure of co-occurrence. We were proven wrong, however, because the performance of the kNN filter rivaled that of the content-based filtering. We had several ideas as to why this might be the case. Perhaps the meta data for each of the songs is highly dependent, which would reduce the amount of information that a vector of metadata could possibly contain. Another possibility is that the metadata is actually extremely diverse, and this diversity makes it difficult to compare vectors. The collaborative filtering would have an advantage in this case, because it doesn’t consider any specific features from the playlist, only how often songs appear with one another. In any case, we feel that these two types of filtering can be combined to maximize the assets that the other lacks.
k-Means Clustering
We were not sure what to expect from the k-Means clustering. While on the one hand we thought it would be a great way to capture higher dimensional similarities across playlists (similar to content-based filtering), there was also the possibility that the most popular tracks would get clustered together, and we’d end up washing out other types of music. Further analysis would need to be done to examine whether this happened, but we were pleased to see that the k-Means clustering outperformed the filtering algorithms, indicating it is even more effective than content-based filtering. This makes sense, as the clustering algorithm iteratively computes similarities as opposed to a simple, single operation that is performed in cosine similarity computations.
ALS Matrix Factorization
ALS Matrix Factorization outperforms other models far in R-precision. We are surprised that it has similar NDCG score with other model approaches we tried, e.g., k-means clustering. NDCG score does not perform as good as we expected, because we expect ALC model to rank the similarity in the suggestion set better because ALC considers similarity and it suggests songs with higher similarity. One of the reasons we suspect is because some of the items have very high similarity scores (e.g., score > 0.999) and therefore, the ranking of the suggestion might be less sensitive. We did not have enough time to cross-validate different lambda to regularize and different number of iterations, but we might get better result if we have more time to tune the model.
Future Work
One model that we didn’t have the chance to implement, was a 2 stage hierarchical model. In the first stage, the model would use one of the filtering techniques described above. At the second stage, we would engineer features and run a gradient boosting algorithm to re-rank the candidate tracks. Additional future work could be done in decreasing the computational complexity of the k-means clustering algorithm, potentially using parallel computing and other multi-threading procedures to allow us to extend our models to the entirety of the million playlist.